Double Integrals

 Plotting the region

clear

clc

% Region of integration

xL=input("Enter lower limit of x")

xU=input("Enter Upper limit of x")

x = linspace(xL, xU);                    % x limits

yL=input("Enter lower limit of y")

yU=input("Enter Upper limit of y")

Li = yU >= yL ;                        % Logical Vector

figure

plot(x,yU,x,yL)

hold on

patch([x(Li) fliplr(x(Li))], [yU(Li) fliplr(yL(Li))], 'b')

hold off

grid

 

Example:

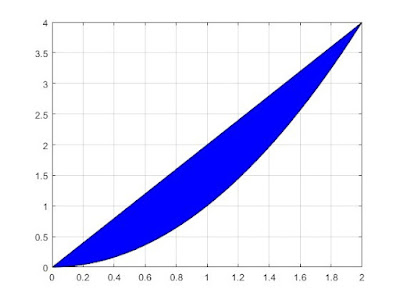
With the program to mark the region of integration in the following double integrals: $$1. \int_0^{2x} \int_{x^2}^{2x} f(x,y) dx dy$$ $$ 2. \int_1^4 \int_{2}^x f(x,y) dx dy$$

Output

1.

Enter lower limit of x: 0

Enter Upper limit of x: 2

Enter lower limit of y: x.^2

Enter Upper limit of y: 2.*x

2.

Enter lower limit of x: 1

Enter Upper limit of x: 4

Enter lower limit of y: 2+0.*x

Enter Upper limit of y: x

NOTE: 

i) If ‘y’ lower limit is constant, give input as yL.*x.

ii) For the polar plot patch won't work (instead of that we need to use polyfill but it is not user-friendly).

Double Integral

 

Syntax	Remark	Syntax	Remark
integral2(f,xL,xU,yL,yU)	f,xL,xU,yL, yU must be function handlers, i.e., use @(x,y), @(x), @(y)	int(int(f,y,yL,yU),x,xL,xU)	f,xL,xU,yL,yU are need not be function handlers, i.e., no need to use @(x,y), @(x), @(y)

 NOTE:

* The order of sending parameter to integral2 is : Integrand, constant lower limit, constant upper limit, 1var lower limit, 1var upper limit

     Example: If x: Const->Const 

                           y: Curve->Curve         then      integral2(f, xL, xU, yL, yU)

                      If  y: Const->Const 

                           x: Curve->Curve         then      integral2(f, yL, yU, xL, xU)

* For the constant limits no need to use function handlers like @(x) or @(y)

* For constant integrand then use use function handlers then add 0.*x.*y

clear

clc

syms x y

f = input("Enter the integrand: ");

disp('f(x,y) :');

disp(f);

 

xL=input("Enter lower limit of x: ");

xU=input("Enter Upper limit of x: ");

yL=input("Enter lower limit of y: ");

yU=input("Enter Upper limit of y: ");

 

d = integral2(f,xL,xU,yL,yU);

disp("Double Integral of f(x,y) :");

disp(d);

 

Write a program to evaluate double integral.

$$\int_1^2 \int_2^3 (x-1/y)^2 dxdy$$ Output: Enter the integrand: @(x,y) (x-1./y).^2 f(x,y) :     @(x,y) (x-1./y).^2 Enter lower limit of x: 1 Enter Upper limit of x: 2 Enter lower limit of y: 2 Enter Upper limit of y: 3 Double Integral of f(x,y) :

$$\int_0^1 \int_x^\sqrt{x} xy dxdy$$ Output:   Enter the integrand: @(x,y)x.*y f(x,y) :     @(x,y)x.*y Enter lower limit of x: 0 Enter Upper limit of x: 1 Enter lower limit of y: @(x) x Enter Upper limit of y: @(x) sqrt(x) Double Integral of f(x,y) :